李士凡：数学冲刺三步走 补漏+破题+抢分

名师档案·李士凡

中小学高级教师，曾长期任教于宿迁中学高中数学学科，教学成果显著。曾多次荣获“高考优秀教师”荣誉称号，并在国家级、省级学术期刊发表多篇教学论文。擅长初高中数学知识的衔接教学，注重在夯实基础的同时培养学生的思维能力和创新意识。

■ 本报记者 蔡依瑾 魏平

中考数学作为学生升学的重要考核科目，如何科学备考成为广大考生关注的焦点。为此，本期特邀宿迁市钟吾初级中学数学名师李士凡，为考生系统讲解中考数学冲刺阶段的备考策略。

基础巩固 查漏补缺是关键

李士凡老师建议，在冲刺阶段，考生应回归教材，重点梳理中低难度题型的知识点，对于基础薄弱的环节，建议通过刷题的方式进行针对性训练。学生可以搜集全省近两年的中考数学真题，只做知识点掌握不熟练的题型。

压轴题突破 掌握方法提效率

中考数学试卷的第27、28题通常为压轴题，分别考查二次函数和平面几何知识。李老师分析指出：二次函数常与面积计算、角度关系、线段最值等问题结合考查，有时还会涉及四边形的相关知识；而平面几何题一般设置三个小问，依次考查全等、相似等几何知识。

针对压轴题的备考策略，李老师强调：务必确保前两问的基础分值，对于第三问，要注意题目设置的递进关系，往往前两问的结论或解题思路能为最后一问提供启示。

典型例题解析

二次函数应用题

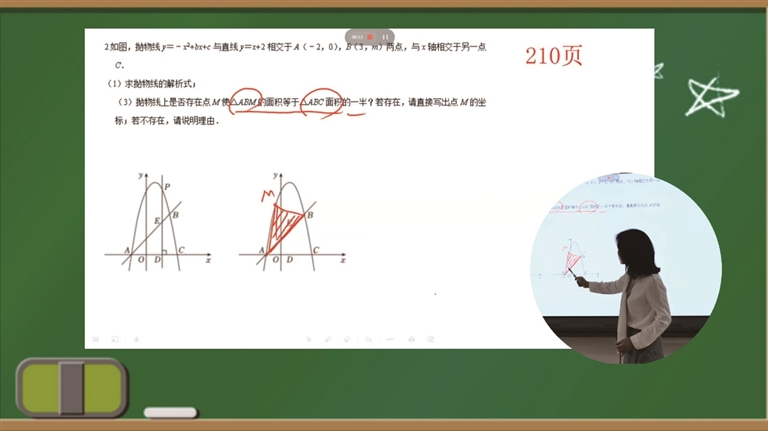
【题目】如图，抛物线y=-x^2+bx+c与直线y=x+2相交于A(-2，0)，B(3，m)两点，与x轴相交于另一点C。

（1）求抛物线的解析式

（2）抛物线上是否存在点M使△ABM的面积等于△ABC面积的一半？若存在，请直接写出点M的坐标；若不存在，请说明理由。

以第2问为例，李老师详细讲解了解题思路：通过条件，我们可以得到固定△ABC的面积和AB段的长度，对于动点M在抛物线上运动的情况，需注意分类讨论。如果M点在抛物线上方的时候，可以采用割补法，过M点，做X轴的垂线，利用水平宽与铅垂高的关系进行转化。此外，也可运用面积公式反推高线长度，再通过三角函数关系转化为线段长度的计算。

平面几何证明题

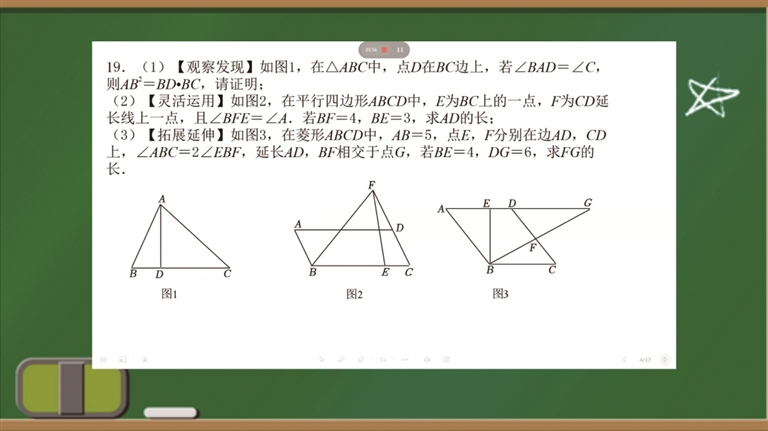
【题目】（1）如图1，在△ABC中，点D在BC边上，若∠BAD=∠C，则AB^2=BD·BC，请证明；

（2）如图2，在平行四边形ABCD中，E为BC上的一点，F为CD延长线上一点，且∠BFE=∠A，若BF=4，BE=3，求AD的长；

（3）如图3，在菱形ABCD中，AB=5，点E，F分别在边AD，CD上∠ABC=2∠EBF，延长AD，BF相交于点G，若BE=4，DG=6，求FG的长。

李老师介绍，平面几何压轴题一般考三个问题，考生做到第三问时往往会摸不到思路，此时可以回头看看第一问和第二问主要目的是什么。以此题为例，主要考的是子母型相似，在解答时，考生可以利用菱形四边相等、对角线平分每一个内角的特征为突破点，∠EBF等于∠ABC的一半，∠DBF加上∠FBC也是∠ABC一半，我们可以得出∠EBD和∠FBC相等，不妨设为a角。我们又知道AG平行BC，那么∠DGB和∠GBC也相等，此时就可以判断出△EDB和△EBG相似，问题也得以解决。

考试时间分配建议

李老师特别提醒考生注意答题节奏，建议将填空题和选择题的答题时间控制在35分钟以内，中档解答题用时不超过45分钟，最后预留40分钟集中攻克两道压轴题。合理的时间分配是确保发挥正常水平的重要因素。

李士凡老师希望同学们在最后的冲刺阶段，能够有针对性地查漏补缺，掌握科学的解题方法，以最佳状态迎接考试。预祝各位考生取得理想成绩，升入心仪的高中。